Hello Programmer

逻辑回归-芯片检测实战

发表于 更新于 分类于

一、基于 chip_test.csv数据集，建立逻辑回归模型（二阶边界），评估模型表现

1、加载数据

1
2
3
4
5
# load the data
import pandas as pd
import numpy as np
data = pd.read_csv('chip_test.csv')
data.head()

2、为数据添加标签

合格即为 true，否则为 false

1
2
3
# add label mask
mask = data.loc[:, 'pass'] == 1
print(~mask)

3、数据的可视化

plt.scatter()原型如下：

1
matplotlib.pyplot.scatter(x, y, s=None, c=None, marker=None, cmap=None, norm=None, vmin=None, vmax=None, alpha=None, linewidths=None, verts=None, edgecolors=None, *, data=None, **kwargs)
  • x、y：表示的是大小为(n, )的数组，也就是我们即将绘制散点图的数据点
  • s：一个实数或者是一个数组大小为(n, )，点的所占的面积大小
  • c：颜色
  • marker：表示的是标记的样式，默认的是 'o'
  • cmap：Colormap实体或者是一个colormap的名字，cmap仅仅当c是一个浮点数数组的时候才使用（默认image.cmap）
  • norm：Normalize实体来将数据亮度转化到0-1之间，也是只有c是一个浮点数的数组的时候才使用（默认colors.Normalize）
  • vmin、vmax：实数，当norm存在的时候忽略（用来进行亮度数据的归一化）
  • alpha：实数，调整线不透明度（0-1）
  • linewidths：也就是标记点的长度
1
2
3
4
5
6
7
8
9
10
11
# visualize the data
%matplotlib inline
from matplotlib import pyplot as plt
fig1 = plt.figure()
passed = plt.scatter(data.loc[:, 'test1'][mask], data.loc[:, 'test2'][mask])
failed = plt.scatter(data.loc[:, 'test1'][~mask], data.loc[:, 'test2'][~mask])
plt.title('test1-test2')
plt.xlabel('test1')
plt.xlabel('test2')
plt.legend((passed, failed), ('passed', 'failed'))
plt.show()

4、定义X、y变量

1
2
3
4
5
6
# define X y
# axis=1代表删掉‘pass’这一列
X = data.drop(['pass'], axis=1)
y = data.loc[:, 'pass']
X1 = data.loc[:, 'test1']
X2 = data.loc[:, 'test2']

5、定义X1方、X2方等变量

DataFrame是Python中Pandas库中的一种数据结构，它类似excel，是一种二维表。DataFrame的单元格可以存放数值、字符串等，这和excel表很像，同时DataFrame可以设置列名columns与行名index，如下通过 X_new设置了五列：

1
2
3
4
5
6
7
# create new data
X1_2 = X1*X1
X2_2 = X2*X2
X1_X2 = X1*X2
X_new = {'X1':X1, 'X2':X2, 'X1_2':X1_2, 'X2_2':X2_2, 'X1_X2':X1_X2}
X_new = pd.DataFrame(X_new)
print(X_new)

6、建立实例并训练模型

1
2
3
4
# establish new model and train
from sklearn.linear_model import LogisticRegression
LR2 = LogisticRegression()
LR2.fit(X_new, y)

7、预测数据

1
2
3
4
5
# predict
from sklearn.metrics import accuracy_score
y2_predict = LR2.predict(X_new)
accuracy2 = accuracy_score(y, y2_predict)
print(accuracy2)

8、获取曲线参数

1
2
3
4
5
# get the params
X1_new = X1.sort_values()
theta0 = LR2.intercept_
theta1, theta2, theta3, theta4, theta5 = LR2.coef_[0][0], LR2.coef_[0][1], LR2.coef_[0][2], LR2.coef_[0][3], LR2.coef_[0][4]
print(theta0, theta1, theta2, theta3, theta4, theta5)

9、构建边界曲线

1
2
3
4
5
# Constructing boundary curve
a =theta4
b = theta5*x1_new + theta2
c = theta0 + theta1*x1_new + theta3*x1_new*x1_new
X_new_boundary = (-b + np.sqrt(b*b - 4*a*c))/(2*a)

10、画曲线

1
2
3
4
5
6
7
8
9
10
# draw the pic
fig4 = plt.figure()
plt.plot(X1_new, X_new_boundary)
passed = plt.scatter(data.loc[:, "test1"][~mask], data.loc[:, "test2"][~mask])  
failed = plt.scatter(data.loc[:, "test1"][mask], data.loc[:, "test2"][mask])
plt.title("test1-test2")
plt.xlabel("test1")
plt.ylabel("test2") 
plt.legend((passed, failed), ('passed', 'failed'))
plt.show()

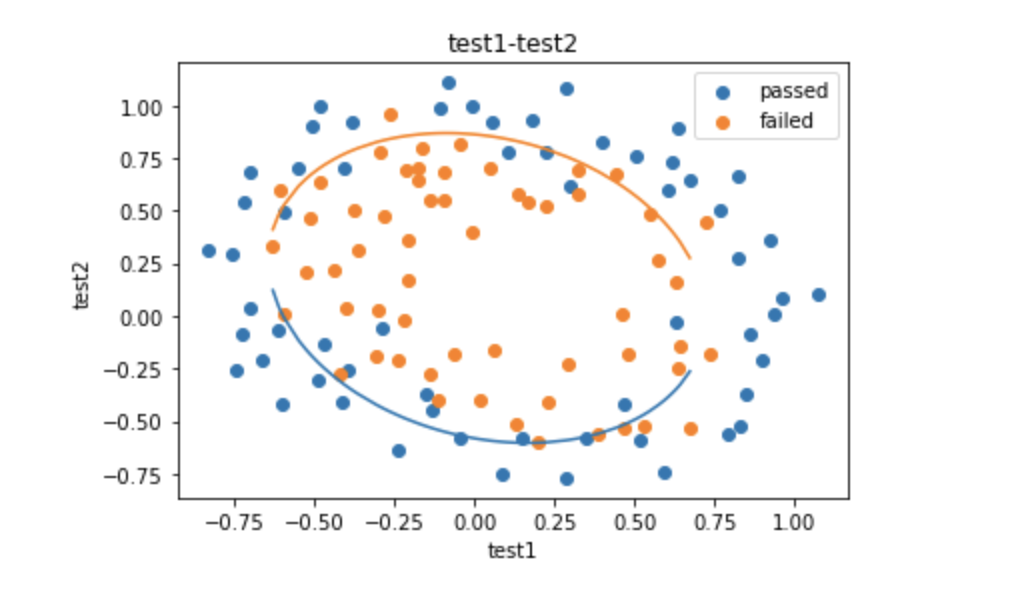
画出来的图像如下（图像并不完整）：

我们只需加上如下代码：

1
2
X_new_boundary_2 = (-b - np.sqrt(b*b - 4*a*c))/(2*a)
plt.plot(X1_new, X_new_boundary_2)

于是画出来的图像便变成如下所示：

二、以函数的方式求解边界曲线

1、定义函数f(x)

1
2
3
4
5
6
7
8
# define f(x)
def f(X1_new):
    a =theta4
    b = theta5*X1_new + theta2
    c = theta0 + theta1*X1_new + theta3*X1_new*X1_new
    X_new_boundary1 = (-b + np.sqrt(b*b - 4*a*c))/(2*a)
    X_new_boundary2 = (-b - np.sqrt(b*b - 4*a*c))/(2*a)
    return X_new_boundary1, X_new_boundary2

2、获取新边界

1
2
3
4
5
6
7
# get X_new_boundary
X2_new_boundary1 = []
X2_new_boundary2 = []
for x in X1_new:
    X2_new_boundary1.append(f(x)[0])
    X2_new_boundary2.append(f(x)[1])
print(X2_new_boundary1, X2_new_boundary2)

3、画图

1
2
3
4
5
6
7
8
9
10
fig5 = plt.figure()
plt.plot(X1_new, X2_new_boundary1)
plt.plot(X1_new, X2_new_boundary2)
passed = plt.scatter(data.loc[:, "test1"][~mask], data.loc[:, "test2"][~mask])  
failed = plt.scatter(data.loc[:, "test1"][mask], data.loc[:, "test2"][mask])
plt.title("test1-test2")
plt.xlabel("test1")
plt.ylabel("test2") 
plt.legend((passed, failed), ('passed', 'failed'))
plt.show()

图像如下（我们发现两边缺了一点）：

4、补数据

将 x轴数据补多一点

1
2
3
4
5
6
7
X1_range = [-0.9 + x/10000 for x in range(0, 19000)]
X1_range = np.array(X1_range)
X2_new_boundary1 = []
X2_new_boundary2 = []
for x in X1_range:
    X2_new_boundary1.append(f(x)[0])
    X2_new_boundary2.append(f(x)[1])

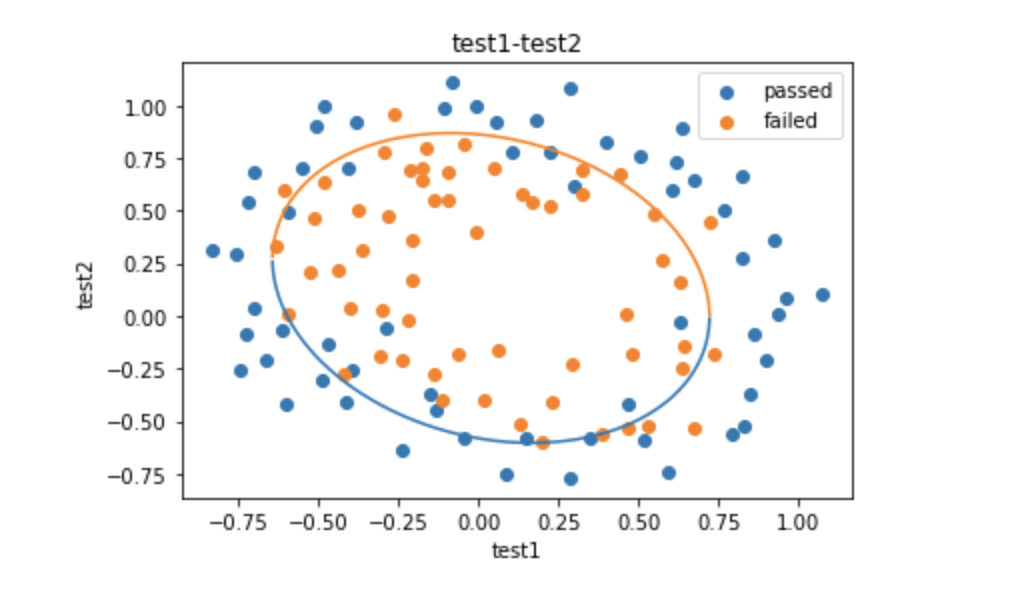
5、描绘出完整的决策边界曲线

1
2
3
4
5
6
7
8
9
10
fig6 = plt.figure()
passed = plt.scatter(data.loc[:, "test1"][~mask], data.loc[:, "test2"][~mask])  
failed = plt.scatter(data.loc[:, "test1"][mask], data.loc[:, "test2"][mask])
plt.plot(X1_range, X2_new_boundary1)
plt.plot(X1_range, X2_new_boundary2)
plt.title("test1-test2")
plt.xlabel("test1")
plt.ylabel("test2")
plt.legend((passed, failed), ('passed', 'failed'))
plt.show()

图如下：