一、关系数据结构及形式化定义
关系数据库系统是支持关系模型的数据库系统,本篇将介绍介绍关系模型。关系模型由 关系数据库、 关系操作集合和 关系完整性约束组成。
1、关系
关系模型只包含单一的数据结构: 关系,下面我们从集合论的角度给出关系数据结构的形式化定义。
a、域(domain)
定义2.1:
域是一组具有相同数据类型的值的集合。例如:自然数、整数、{0、1}、{男、女}
b、笛卡尔积(cartesian product)
定义2.2:给定一组域D1、D2、、、D3,则该域的笛卡尔积为:
D1 x D2 x ··· x Dn = {(d1, d2, ··· dn) | di ∈ Di, i = 1, 2, ··· n }
其中,每一个元素 (d1, d2, ··· dn)叫做一个 n元组(n-tuple),或简称 元组(tuple),元素中的每一个值 di叫做一个 分量(component)。一个域允许的不同的取值个数称为这个域的基数(cardinal number)。
笛卡尔积可表示为一张二维表,表中的每一行对应一个元组,表中的每一列都来组一个域,如下给出三个域:

则 D1、D2、D3笛卡尔积为:

其中 (张清玫, 计算机专业, 李勇)是元组, 张清玫、计算机砖业都是分量。该笛卡尔积的基数为 2x2x3=12,也就是说共有12个元组,组成二维表如下:
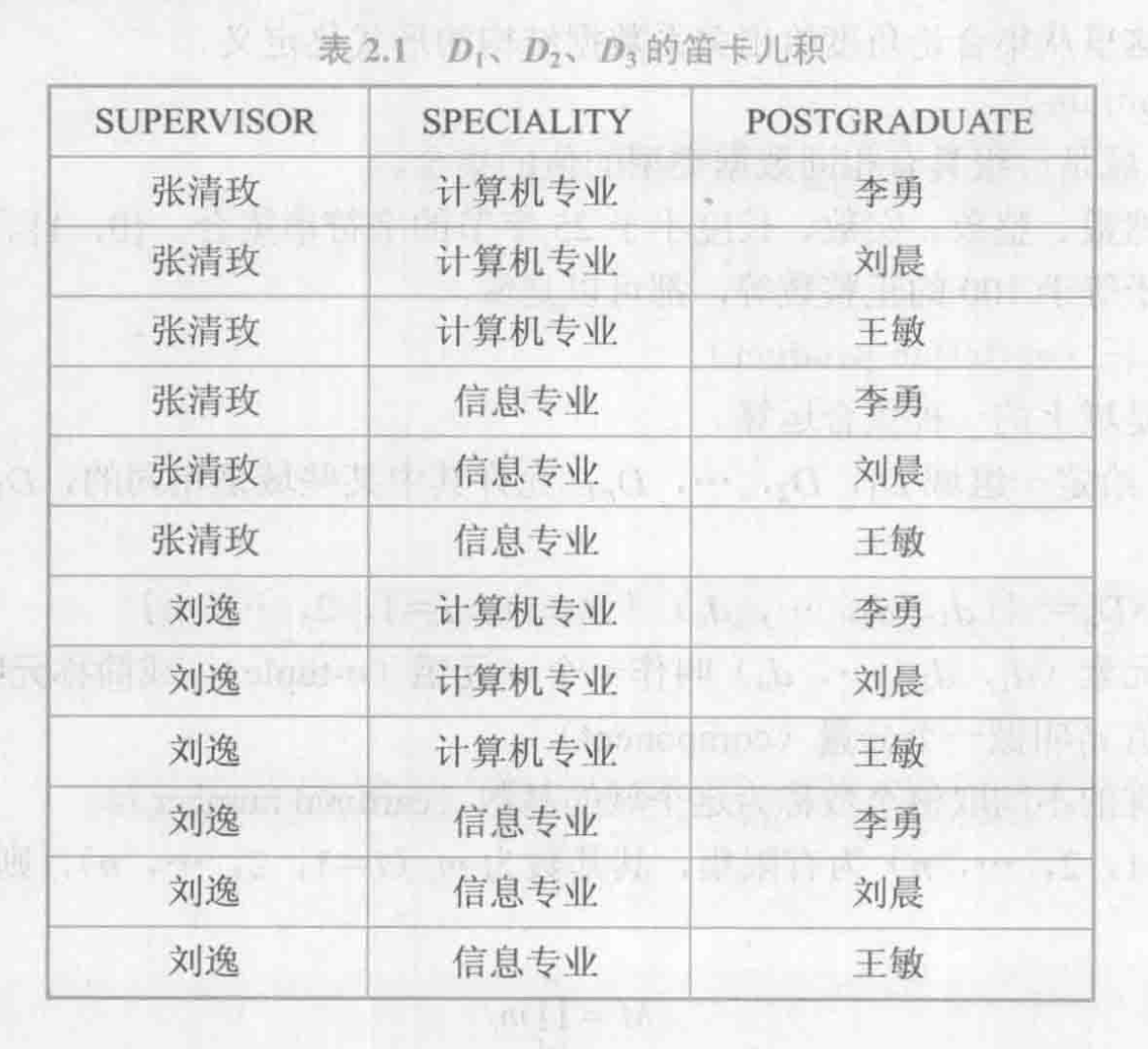
c、关系(relation)
定义2.3:
D1 x D2 x ··· x Dn的子集叫做在域D1, D2, ··· Dn上的关系,表示为R(D1, D2, ··· Dn),这里的R表示关系的名称,n是关系的目或度(degree)

若关系中的某一组属性能够唯一的标识一个元组,而其子集不能,则称该属性组为 候选码(candadate key),若一个关系有多个 候选码,则选定其中一个为主码(primary key)。
候选码的诸属性称为 主属性(prime attribute)。不包含在任何 候选码中的属性称为 非主属性(non-prime attribute)或者 非码属性(non-key attribute)。
在最简单的情况下, 候选码只有一个属性,在最极端的情况下,关系模式中的所有属性是这个关系模式的候选码,称为 全码(all-key)。关系可以有三种类型: 基本关系(通常又称为基本表或基表)、 查询表和 视图表。基本关系具有以下六种性质:

关系的每一个分量为一个不可分的数据项,如下表不符合规范化的要求(表中有表):
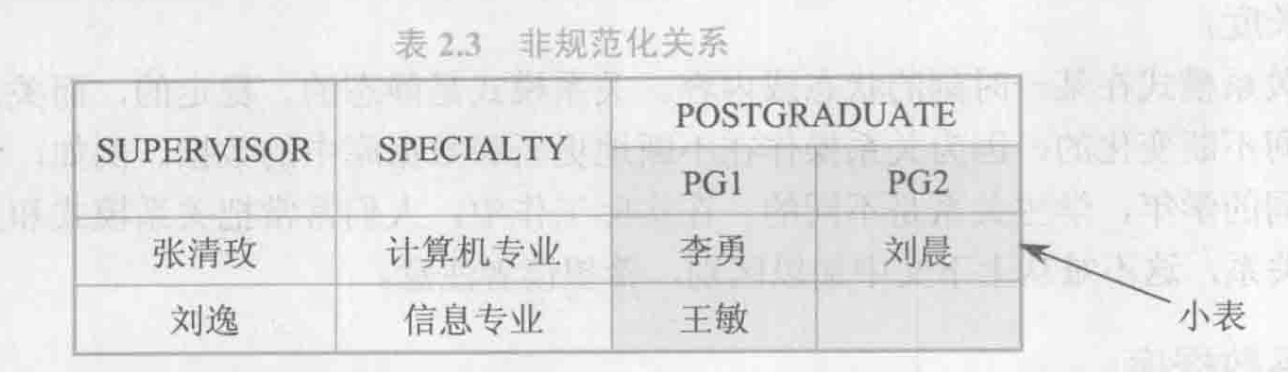
2、关系模式
关系的描述称为
关系模式(relation schema),它可以形式化的表示为:R(U, D, DOM, F),其中R为关系名,U为组成该关系的属性名集合,D为U所来自的域,DOM为属性向域的映像集合,F为属性间数据的依赖关系集合。
关系是 关系模式在某一时刻的状态或内容,关系模式是静态的稳定的,而关系动态的随时间不断变化的。
3、关系数据库
关系数据库也有值和型之分:
关系数据库的型也称为关系数据库模式,是对关系数据库的描述关系数据库的值是这些关系模式在某一时刻对应的关系集合,通常就称为关系数据库
4、关系模型的存储结构
在关系数据库的物理组织中,有的关系数据库管理系统中的一个表对应一个操作系统文件,将物理数据组织交给操作系统;有的从操作系统申请若干个大的文件,自己划分空间,组织表、索引等存储结构,进行存储管理。
二、关系操作
关系模型给出了关系操作能力的说明,但没有对关系数据库管理语言做具体的语法要求。
1、基本的关系操作
关系模型中常用的操作为:查询(Query)、插入(Insert)、 删除(Delete)、修改(Update)
查询操作又分为:选择(select)、 投影(project)、连接(join)、除(divide)、并(union)、差(except)、交(intersection)和笛卡尔积
关系操作的对象和结果都是集合
2、关系数据语言的分类

三、关系的完整性
关系模型的完整性规则是对关系的某种约束条件
关系模型中有三类完整性约束:实体完整性(entity integrity)、参照完整性(referential integrity)、用户定义的完整性(user-defined integrity),其中前两个是关系模型必须满足的完整性约束条件,被称为关系的两个不变性
1、实体完整性
规则2.1 实体完整性规则:若属性(指一个或一组属性)A是基本关系R的主属性,则A不能取空值(null value)

说白了就是主属性不能为空
